本文全面剖析滑动轴承相关知识，深入阐释动压润滑原理，着重解读直接刚度与交叉刚度含义，并结合实例，详细说明利用扰动法求解这些刚度参数的步骤，为滑动轴承的深入研究与工程应用筑牢理论根基。

一、滑动轴承动压润滑原理

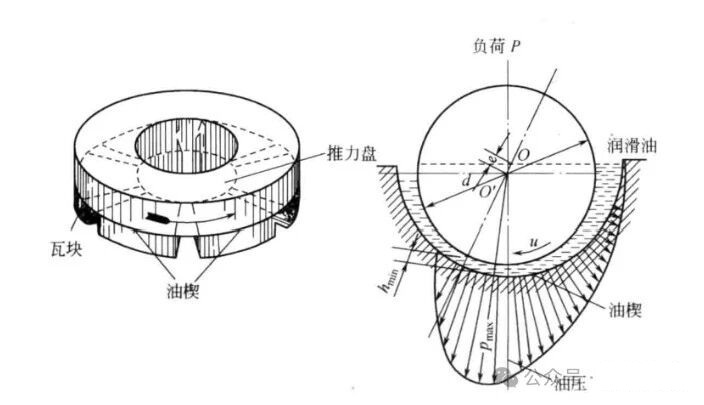
启动时，滑动轴承的轴颈转速低，在摩擦力作用下沿轴承内壁上爬，此时处于边界润滑，摩擦损耗大。随着转速上升，轴颈带动润滑油从间隙大处流向间隙小处。根据流体力学原理，在收敛间隙内，润滑油受挤压形成压力油膜。当油膜压力足以抗衡轴颈载荷时，轴颈稳定在特定偏心位置旋转，轴颈与轴承内壁被压力油膜隔开，实现动压润滑。该油膜承载能力强，能大幅降低轴颈与轴承间的磨损和摩擦功耗，提高轴承工作性能和寿命。

二、滑动轴承刚度参数及其含义

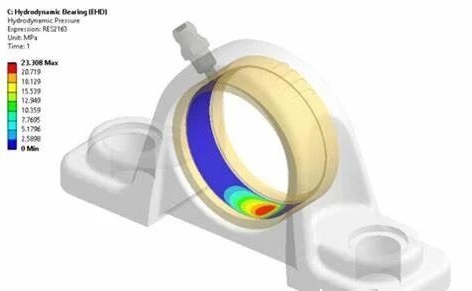
在旋转机械中，滑动轴承作为关键部件，其刚度特性对转轴动力学有着极为显著的影响。滑动轴承刚度，决定了其为转轴提供支撑的强度和稳定性 。当滑动轴承刚度不足时，在转轴高速旋转过程中，受到不平衡力、摩擦力等多种载荷作用下，轴承无法给予转轴足够的约束。这会导致转轴在运转时发生较大变形，进而使转轴的振动响应加剧，直接影响旋转机械的稳定性和可靠性。

在进行转轴的变形仿真时，滑动轴承刚度是不可或缺的重要参数。若在仿真中设定的滑动轴承刚度与实际不符，会使仿真结果严重偏离真实情况，无法准确预测转轴在实际工况下的变形状态，可能导致旋转机械在设计阶段对潜在的安全隐患和性能问题预估不足，最终影响设备的正常运行和使用寿命。

（一）直接刚度

1. x方向径向直接刚度（K_{xx}）：指在x方向上，单位x向位移所引发的x方向径向力变化。它体现了滑动轴承抵抗x方向变形的能力，K_{xx}越大，在相同x向载荷下，轴承在x方向的位移越小。比如在精密镗床的主轴滑动轴承中，高K_{xx}能确保镗刀在x向进给时保持精准位置，提升镗孔精度。

2. y方向径向直接刚度（K_{yy}）：表示在y方向上，单位y向位移所产生的y方向径向力变化。反映了滑动轴承抵抗y方向变形的能力，对于承受y向载荷的轴系，较大的K_{yy}可保证轴系稳定。如在纺织机械的罗拉轴滑动轴承中，足够的K_{yy}能防止罗拉在转动时出现y向跳动，保证纱线质量。

（二）交叉刚度

1. x-y交叉刚度（K_{xy}）：当轴颈在x方向产生单位位移时，所引起的y方向径向力变化。这一参数反映了x方向位移与y方向径向力之间的耦合关系。在高速离心机的转鼓轴滑动轴承中，若K_{xy}较大，x方向的微小位移可能引发较大的y向径向力，导致转鼓振动加剧，影响离心机的正常运行。

2. y-x交叉刚度（K_{yx}）：指轴颈在y方向产生单位位移时，所引起的x方向径向力变化。体现了y方向位移与x方向径向力的耦合。例如在印刷机的滚筒轴滑动轴承中，y方向的位移可能因K_{yx}的存在而产生x方向的径向力，进而影响滚筒的平行度和印刷质量。

三、采用扰动法求各个刚度参数实例

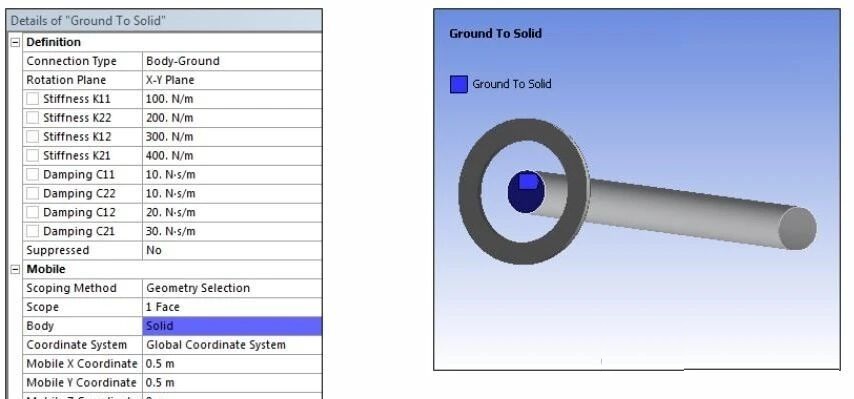
扰动法求滑动轴承刚度的核心思路基于力与位移的变化关系。在初始稳定工况下，记录滑动轴承轴颈所受的载荷以及对应的位置 。随后，对轴颈施加一个精心控制的微小扰动，如在径向或轴向给予微小位移扰动。在施加扰动后，精确测量轴颈所受力的变化情况。根据刚度的定义，即单位位移变化所引起的力的改变量，将测量得到的力的变化值除以所施加的微小位移扰动值，就可以计算出相应方向的刚度。对于交叉刚度，则是在某一方向施加扰动位移，测量另一方向力的变化来求解。通过这种方式，能够较为准确地获取滑动轴承在不同方向的刚度参数，为分析滑动轴承性能及轴系动力学特性提供关键数据支持。

假定有一滑动轴承，已知其几何尺寸、润滑油特性、轴颈转速及载荷等初始条件。可通过仿真或实验，确定刚度参数的大小，现分别举例说明。

（一）直接刚度求解

x方向径向直接刚度（K_{xx}）：记录轴颈初始所受x方向径向载荷F_{x0}和x方向位置x_0。对轴颈施加微小x向扰动位移dx，测量此时轴颈所受的x方向径向力F_{x1}。根据公式K_{xx}=(F_{x1}-F_{x0})/dx。若初始F_{x0}为500N ，dx为0.01mm ，F_{x1}变为530N ，则K_{xx}==3000N/mm。

（二）交叉刚度求解

1. x-y交叉刚度（K_{xy}）：先记录轴颈初始x方向位置x_0和y方向径向力F_{y0}。对轴颈施加微小x向扰动位移dx，测量扰动后产生的y方向径向力F_{y1}。K_{xy}=(F_{y1}-F_{y0})/dx。如施加dx = 0.01mm ，F_{y0}为100N ，F_{y1}变为120N ，则K_{xy}=2000N/mm。

四、刚度参数在轴的转子动力学分析中的应用

（1）建立动力学方程

将滑动轴承的刚度参数融入轴的转子动力学模型中，构建轴系的运动微分方程。以Jeffcott转子模型为基础，考虑x和y两个方向的运动，方程可表示为：

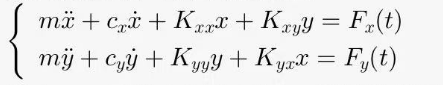
其中，m是轴上集中质量，\ddot{x}和\ddot{y}分别是x和y方向的加速度，\dot{x}和\dot{y}是速度，c_{x}和c_{y}为阻尼系数，F_{x}(t)和F_{y}(t)是x和y方向随时间变化的外力。刚度参数K_{xx}、K_{yy}、K_{xy}和K_{yx}直接影响方程中弹性力项，决定轴系在不同方向位移下所受恢复力的大小和耦合关系。

（2）临界转速计算

在转子动力学分析中，临界转速是重要指标。通过将刚度参数代入特征值问题求解，可以得到轴系的临界转速。将运动微分方程写成矩阵形式,通过求解特征方程，可得到轴系的固有频率，对应不同阶次的固有频率，其中使轴系发生共振的转速即为临界转速。

刚度参数的变化会改变刚度矩阵[K]，从而影响临界转速的计算结果。例如，当K_{xx}增大时，轴系在x方向的刚度增强，对应一阶临界转速通常会升高，表明轴系在高速运转时抵抗弯曲变形的能力增强。

（3）稳定性分析

利用刚度参数判断轴系的稳定性。根据劳斯-胡尔维茨稳定性判据，对运动微分方程对应的特征方程进行分析。刚度参数不仅影响特征根的实部和虚部，还通过交叉刚度体现的耦合作用，影响轴系在不同方向运动的相互影响。若交叉刚度K_{xy}或K_{yx}过大，可能导致轴系在某些转速下出现不稳定的振动模态，即特征根实部大于零，轴系振动随时间不断发散。通过分析刚度参数对稳定性的影响，可以优化滑动轴承设计，调整刚度参数，使轴系在工作转速范围内保持稳定运行。